Unlocking The Secrets: A Comprehensive Guide To The Pythagorean Theorem Trigonometry Proof

Mathematics is a universal language, a fascinating field that connects different branches of knowledge through its timeless principles and theorems. Among these principles, the Pythagorean Theorem stands out as one of the most well-known and widely applied theorems in geometry. It is a fundamental principle that relates the sides of a right triangle, providing the mathematical framework for many real-world applications. While the theorem itself is straightforward, the intriguing part lies in its numerous proofs, one of which is the trigonometry proof. This article delves into the Pythagorean Theorem Trigonometry Proof, offering a detailed exploration of its intricacies, applications, and historical significance.

The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, has been a cornerstone in the study of mathematics and geometry for centuries. It asserts that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. While the theorem is primarily associated with geometry, its proof using trigonometry adds another layer of understanding and demonstrates the interconnectedness of different mathematical disciplines. This trigonometric approach not only reinforces the theorem's validity but also highlights the elegance and versatility of mathematical reasoning.

In this comprehensive guide, we will explore the Pythagorean Theorem Trigonometry Proof in detail, breaking down the mathematical concepts and principles involved. We will begin by revisiting the basics of the Pythagorean Theorem and its historical context before diving into the trigonometric proof. Along the way, we will examine how trigonometry provides a unique perspective on this classic theorem, enhancing our appreciation for its role in mathematics. By the end of this article, readers will have a deeper understanding of the theorem's significance, its proof using trigonometry, and the broader implications for both mathematics and real-world applications.

Table of Contents

• Understanding the Basics of the Pythagorean Theorem
• Historical Context and Significance
• Trigonometry and the Pythagorean Theorem
• The Trigonometry Proof in Detail
• Applications of the Trigonometry Proof
• Comparison with Other Proofs
• Visualizing the Trigonometry Proof
• Educational Implications
• Common Misconceptions
• Real-World Examples and Applications
• Advancements in Mathematics through the Pythagorean Theorem
• The Future of Mathematics and Geometry
• Frequently Asked Questions
• Conclusion

Understanding the Basics of the Pythagorean Theorem

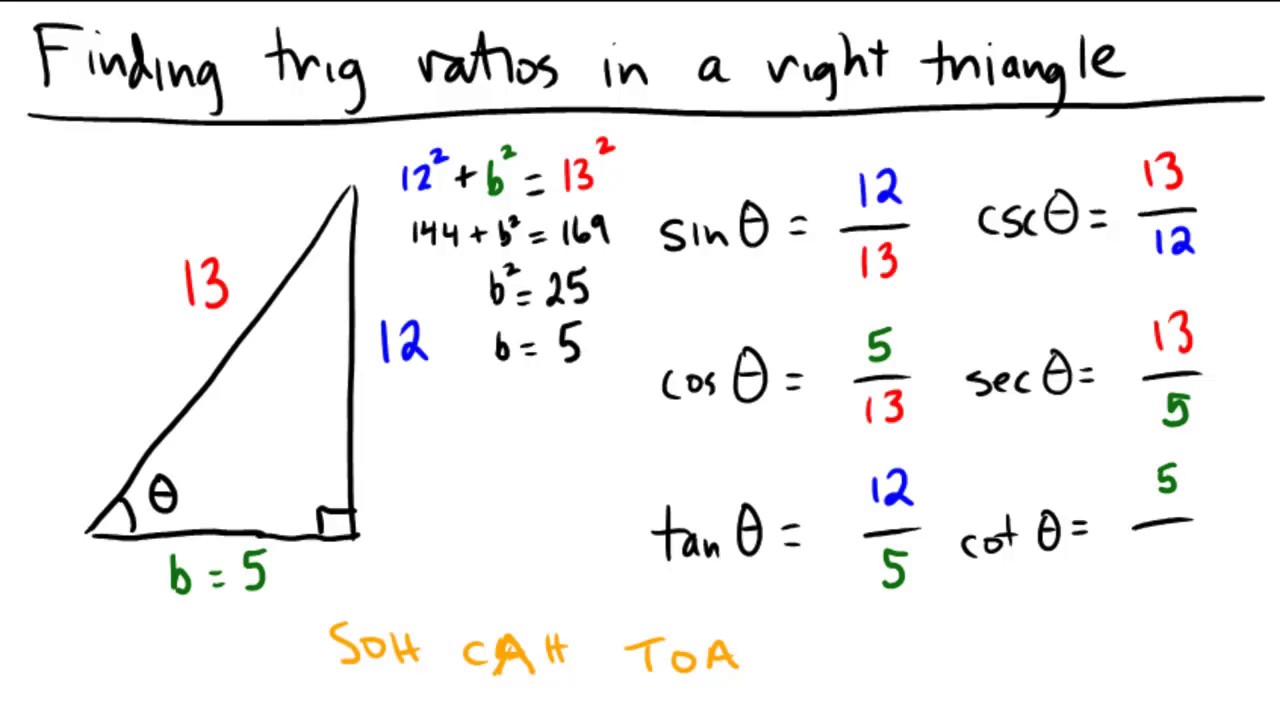
The Pythagorean Theorem is a fundamental principle in mathematics that establishes a relationship between the three sides of a right triangle. This theorem states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Mathematically, it is expressed as \(a^2 + b^2 = c^2\), where \(c\) is the length of the hypotenuse, and \(a\) and \(b\) are the lengths of the other two sides.

This theorem is not only applicable in the realm of pure mathematics but also in various practical fields such as architecture, engineering, and computer science. Its simplicity and wide applicability make it an essential tool for anyone working with measurements and dimensions.

To fully appreciate the Pythagorean Theorem, it is crucial to understand the properties of right triangles and how the theorem applies to these shapes. Right triangles are characterized by one angle measuring 90 degrees, and the Pythagorean Theorem helps us solve problems related to their dimensions. This foundational knowledge sets the stage for exploring the theorem's proof using trigonometry, which will be discussed later in the article.

Historical Context and Significance

The origins of the Pythagorean Theorem can be traced back to ancient civilizations, with evidence of its use found in Babylonian, Indian, and Chinese mathematics. However, it is most famously attributed to the Greek mathematician Pythagoras, who lived around 570-495 BCE. Pythagoras is credited with formalizing the theorem and introducing it to the Western world through his mathematical school.

Pythagoras and his followers, known as the Pythagoreans, believed in the intrinsic connection between mathematics and the natural world. They saw numbers and mathematical relationships as the underlying principles of reality, and the Pythagorean Theorem became a symbol of this belief. The theorem's elegance and simplicity have made it a timeless mathematical truth, inspiring countless mathematicians throughout history.

Despite its association with Pythagoras, the theorem was known and used by other cultures long before his time. The ancient Babylonians, for example, had knowledge of the theorem and used it in their astronomical calculations. Similarly, ancient Indian mathematicians utilized the theorem in their work on geometry and algebra. This widespread use underscores the theorem's universal significance and its foundational role in the development of mathematical thought.

Trigonometry and the Pythagorean Theorem

Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of triangles. It provides tools and methods for solving problems involving triangles, making it a valuable complement to the Pythagorean Theorem. The connection between trigonometry and the Pythagorean Theorem is particularly evident in right triangles, where trigonometric functions such as sine, cosine, and tangent are defined.

In a right triangle, the sine of an angle is the ratio of the length of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side. These trigonometric functions are directly related to the sides of the triangle, and their relationships are governed by the Pythagorean Theorem.

The trigonometric proof of the Pythagorean Theorem leverages these relationships to demonstrate the theorem's validity. By using trigonometry, we can derive the theorem from the fundamental properties of trigonometric functions, providing a different perspective on this classic mathematical principle. This approach highlights the interconnectedness of mathematical concepts and reinforces the theorem's importance in the study of geometry and trigonometry.

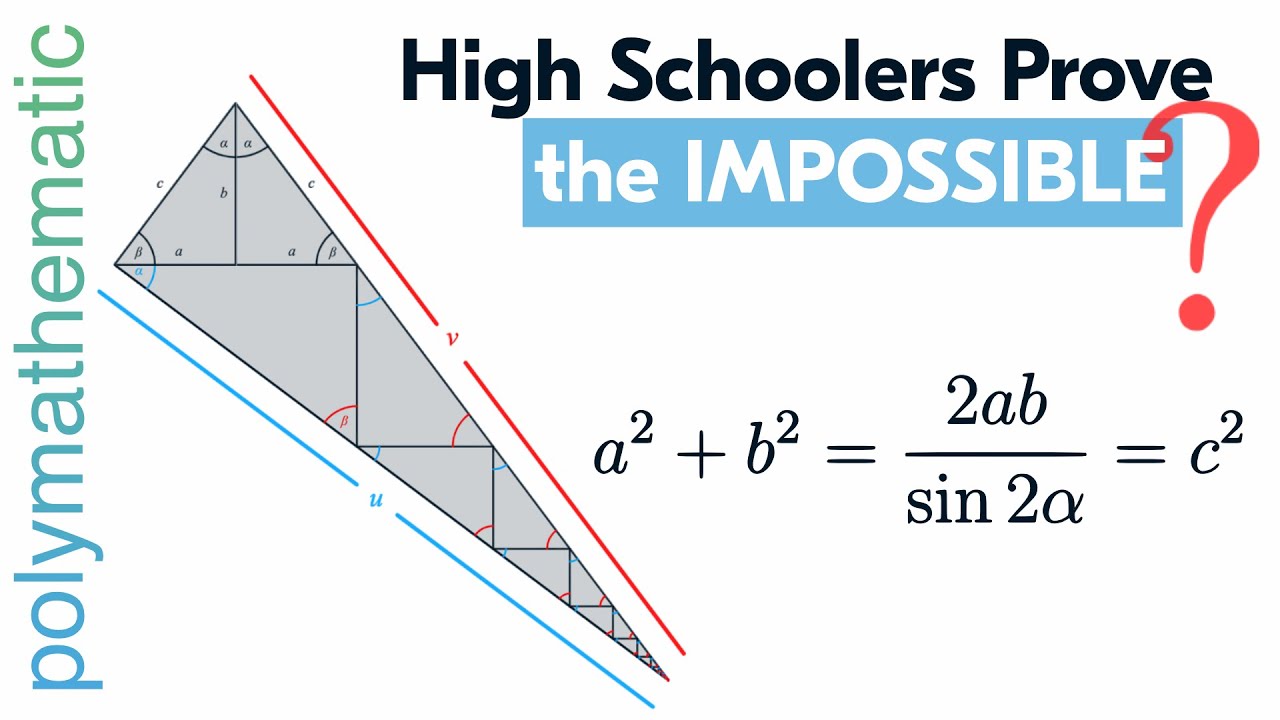
The Trigonometry Proof in Detail

The trigonometry proof of the Pythagorean Theorem is a compelling demonstration of how trigonometric principles can be used to validate geometric truths. This proof utilizes the relationships between the sides and angles of a right triangle and the fundamental trigonometric identities to establish the theorem.

Consider a right triangle with angles \(A\), \(B\), and \(C\), where \(C\) is the right angle. Let the sides opposite these angles be \(a\), \(b\), and \(c\) respectively, with \(c\) being the hypotenuse. According to the trigonometric definitions, we have:

• \(\sin A = \frac{a}{c}\)
• \(\cos A = \frac{b}{c}\)

Using the fundamental trigonometric identity for sine and cosine, we know that:

\(\sin^2 A + \cos^2 A = 1\)

Substituting the expressions for sine and cosine, we get:

\(\left(\frac{a}{c}\right)^2 + \left(\frac{b}{c}\right)^2 = 1\)

Simplifying, we find:

\(\frac{a^2}{c^2} + \frac{b^2}{c^2} = 1\)

Multiplying through by \(c^2\), we arrive at the familiar form of the Pythagorean Theorem:

\(a^2 + b^2 = c^2\)

This trigonometric proof not only confirms the theorem but also illustrates the power of trigonometry in solving geometric problems. By using trigonometric identities and relationships, we gain a deeper understanding of the theorem's foundation and its applications in both mathematics and the real world.

Applications of the Trigonometry Proof

The trigonometry proof of the Pythagorean Theorem is not just an academic exercise; it has practical applications in various fields. Its use in solving problems related to right triangles makes it invaluable in areas such as engineering, physics, architecture, and computer graphics.

In engineering, the theorem and its trigonometric proof are used to design and analyze structures, ensuring stability and safety. For example, in civil engineering, the theorem helps calculate the lengths and angles of support beams and trusses, which are crucial for maintaining the structural integrity of buildings and bridges.

In physics, the theorem is used to solve problems involving vectors and forces. By breaking down vectors into their components, physicists can apply the Pythagorean Theorem to determine the resultant force or velocity in a given system. This application is essential in fields such as mechanics, where understanding the relationship between forces is critical.

Architects use the theorem to create accurate blueprints and designs, ensuring that structures are built to precise specifications. In addition, the theorem is used in computer graphics to calculate distances and angles in 3D modeling, enabling the creation of realistic digital environments.

Overall, the trigonometry proof of the Pythagorean Theorem is a powerful tool that extends beyond theoretical mathematics, offering practical solutions to real-world challenges. Its versatility and applicability underscore the value of understanding and mastering this fundamental mathematical concept.

Comparison with Other Proofs

The Pythagorean Theorem is one of the most proven theorems in mathematics, with hundreds of different proofs documented throughout history. Each proof offers a unique perspective on the theorem, highlighting different aspects of its mathematical beauty and significance. The trigonometry proof stands out for its use of trigonometric functions and identities, but it is just one of many ways to demonstrate the theorem's validity.

One of the most famous proofs is attributed to the ancient Greek mathematician Euclid, who used geometric constructions to prove the theorem in his seminal work, "Elements." Euclid's proof involves constructing squares on each side of the right triangle and demonstrating their areas' relationship, providing a purely geometric approach to the theorem.

Another notable proof is the algebraic proof, which involves manipulating algebraic expressions to arrive at the theorem's equation. This proof is often taught in schools due to its simplicity and accessibility, making it an excellent introduction to algebraic reasoning.

There are also numerous visual proofs, which use diagrams and illustrations to convey the theorem's truth intuitively. These proofs are particularly effective in educational settings, as they help students grasp the concept without relying heavily on mathematical notation.

Each proof of the Pythagorean Theorem has its merits, and comparing them provides valuable insights into different mathematical approaches and techniques. The trigonometry proof, with its reliance on trigonometric functions and identities, offers a unique perspective that complements other proofs and enriches our understanding of this fundamental theorem.

Visualizing the Trigonometry Proof

Visualizing mathematical concepts can be a powerful tool for understanding and retention. The trigonometry proof of the Pythagorean Theorem can be effectively visualized using diagrams and illustrations that depict the relationships between the sides and angles of a right triangle.

A common way to visualize the proof is by drawing a right triangle and labeling its sides and angles. By representing the trigonometric functions sine and cosine as ratios of the sides, we can create a visual representation of the relationships that underpin the proof. This diagram can then be used to illustrate the trigonometric identity \(\sin^2 A + \cos^2 A = 1\) and demonstrate how it leads to the Pythagorean Theorem.

Another visualization technique involves using dynamic geometry software, which allows users to manipulate the triangle's vertices and observe how the relationships between the sides and angles change. This interactive approach can provide a deeper understanding of the theorem by allowing users to experiment with different configurations and explore the underlying mathematical principles.

Visual aids can also include animations that show the step-by-step progression of the trigonometry proof, highlighting the logical flow of the argument. These animations can be particularly helpful for students who benefit from seeing the proof unfold in a dynamic and engaging way.

Overall, visualizing the trigonometry proof of the Pythagorean Theorem can enhance comprehension and make the concept more accessible to learners of all levels. By incorporating visual elements into the learning process, we can foster a more intuitive and holistic understanding of this classic mathematical principle.

Educational Implications

The Pythagorean Theorem and its trigonometry proof have significant educational implications, serving as foundational concepts in the teaching of mathematics. Understanding these principles is crucial for students as they progress through their mathematical education and encounter more advanced topics.

Teaching the Pythagorean Theorem provides an opportunity to introduce students to the beauty and elegance of mathematical reasoning. By exploring different proofs, including the trigonometry proof, educators can demonstrate the diversity of mathematical thought and the various ways to approach a problem. This exposure encourages critical thinking and problem-solving skills, which are essential for success in mathematics and beyond.

The trigonometry proof, in particular, offers a valuable introduction to trigonometric concepts and functions. By using this proof as a teaching tool, educators can help students develop a solid understanding of trigonometry and its applications. This foundation is essential for students who will go on to study subjects such as calculus, physics, and engineering, where trigonometry plays a critical role.

Incorporating visual aids and interactive tools into the teaching of the Pythagorean Theorem and its trigonometry proof can enhance student engagement and comprehension. By making the learning process more dynamic and interactive, educators can create a more inclusive and effective learning environment that caters to a variety of learning styles.

Ultimately, the educational implications of the Pythagorean Theorem and its trigonometry proof extend beyond mathematics, fostering a love for learning and an appreciation for the power of mathematical reasoning. By instilling these values in students, educators can prepare them for success in a wide range of fields and endeavors.

Common Misconceptions

Despite its simplicity, the Pythagorean Theorem is often subject to misunderstandings and misconceptions, particularly when it comes to its trigonometry proof. By addressing these misconceptions, we can help learners develop a more accurate and comprehensive understanding of the theorem and its applications.

One common misconception is that the Pythagorean Theorem only applies to right triangles with integer side lengths, known as Pythagorean triples. In reality, the theorem applies to all right triangles, regardless of the specific measurements of their sides. This misconception can be addressed by providing examples of right triangles with non-integer side lengths and demonstrating how the theorem still holds true.

Another misconception is that the trigonometry proof of the Pythagorean Theorem is overly complex or difficult to understand. While the proof does involve trigonometric functions and identities, it can be made accessible through clear explanations and visual aids. Educators can help students overcome this misconception by breaking down the proof into manageable steps and using diagrams to illustrate the relationships between the sides and angles of the triangle.

Some learners may also mistakenly believe that the Pythagorean Theorem is only relevant in academic settings and has little practical application. In reality, the theorem is used extensively in various fields, as discussed earlier in this article. By providing real-world examples and applications, educators can help students appreciate the theorem's relevance and importance.

By addressing these and other misconceptions, we can help learners build a more accurate and nuanced understanding of the Pythagorean Theorem and its trigonometry proof. This understanding is essential for success in mathematics and for fostering a lifelong appreciation for the power and beauty of mathematical reasoning.

Real-World Examples and Applications

The Pythagorean Theorem and its trigonometry proof have a wide range of real-world applications, making them valuable tools for solving practical problems. Here are some examples of how the theorem is used in various fields:

• Architecture and Construction: The Pythagorean Theorem is used to calculate the dimensions and angles of structures, ensuring that they are built to precise specifications. It is also used to determine the lengths of diagonals in rectangular layouts, which is essential for tasks such as laying out floor tiles or constructing roofs.
• Navigation and Surveying: Surveyors use the theorem to measure distances and angles when mapping out land. In navigation, the theorem is used to calculate the shortest distance between two points, which is crucial for determining travel routes and plotting courses.
• Physics and Engineering: The theorem is used to analyze forces and vectors, helping engineers design stable structures and systems. It is also used in physics to calculate the resultant force or velocity in a given system, which is essential for understanding motion and dynamics.
• Computer Graphics: In computer graphics, the theorem is used to calculate distances and angles in 3D modeling, enabling the creation of realistic digital environments. It is also used in algorithms for rendering and animation, helping to create smooth and accurate visual effects.
• Sports and Recreation: The theorem is used in sports to calculate distances and trajectories, helping athletes optimize their performance. For example, in basketball, the theorem can be used to determine the optimal angle and force needed to make a shot.

These examples illustrate the versatility and practicality of the Pythagorean Theorem and its trigonometry proof. By understanding and applying these concepts, individuals can solve a wide range of problems and make informed decisions in various fields.

Advancements in Mathematics through the Pythagorean Theorem

The Pythagorean Theorem has played a significant role in the advancement of mathematics, serving as a foundation for many mathematical discoveries and developments. Its influence can be seen in various branches of mathematics, from geometry to algebra to trigonometry.

In geometry, the Pythagorean Theorem is used to derive other geometric principles and theorems. For example, it is the basis for the distance formula, which calculates the distance between two points in a coordinate plane. It is also used to prove the properties of similar triangles and to derive the formulas for the area and perimeter of various shapes.

In algebra, the Pythagorean Theorem is used to solve quadratic equations and to understand the properties of complex numbers. It is also the foundation for the concept of Pythagorean triples, which are sets of three positive integers that satisfy the theorem's equation.

In trigonometry, the Pythagorean Theorem is used to derive the fundamental trigonometric identities, such as \(\sin^2 A + \cos^2 A = 1\). These identities are essential for solving trigonometric equations and for understanding the relationships between angles and sides in triangles.

The Pythagorean Theorem has also inspired advancements in other areas of mathematics, such as calculus and topology. Its influence can be seen in the development of mathematical concepts such as limits, continuity, and the concept of space.

Overall, the Pythagorean Theorem has been a driving force in the advancement of mathematics, inspiring new discoveries and developments across various branches of the field. Its enduring significance underscores its importance as a fundamental mathematical principle.

The Future of Mathematics and Geometry

As we look to the future, the Pythagorean Theorem and its trigonometry proof will continue to play a vital role in the study and advancement of mathematics and geometry. Their enduring significance and versatility make them essential tools for solving problems and making discoveries in various fields.

In the field of education, the Pythagorean Theorem will continue to be a foundational concept in the teaching of mathematics. Its simplicity and elegance make it an excellent introduction to the beauty and power of mathematical reasoning, helping to inspire the next generation of mathematicians and scientists.

In the field of technology, the Pythagorean Theorem will continue to be used in the development of new tools and systems. Its applications in computer graphics, engineering, and physics make it an essential tool for solving practical problems and making advancements in these fields.

In the field of research, the Pythagorean Theorem will continue to inspire new discoveries and developments in mathematics. Its influence can be seen in the development of new mathematical concepts and theories, as well as in the exploration of new areas of study.

Overall, the Pythagorean Theorem and its trigonometry proof will continue to be a driving force in the advancement of mathematics and geometry. Their enduring significance and versatility make them essential tools for solving problems and making discoveries in various fields, ensuring their continued relevance and importance in the future.

Frequently Asked Questions

Q: What is the Pythagorean Theorem Trigonometry Proof?

A: The Pythagorean Theorem Trigonometry Proof is a demonstration of the Pythagorean Theorem using trigonometric functions and identities. It leverages the relationships between the sides and angles of a right triangle to establish the theorem's validity.

Q: Why is the Pythagorean Theorem important?

A: The Pythagorean Theorem is important because it provides a fundamental relationship between the sides of a right triangle. Its simplicity and wide applicability make it an essential tool for solving problems in various fields, including mathematics, engineering, physics, and architecture.

Q: Are there other proofs of the Pythagorean Theorem?

A: Yes, there are numerous proofs of the Pythagorean Theorem, each offering a unique perspective on the theorem. These include geometric proofs, algebraic proofs, and visual proofs, among others.

Q: How is the Pythagorean Theorem used in real-world applications?

A: The Pythagorean Theorem is used in various real-world applications, such as architecture, navigation, engineering, computer graphics, and sports. It helps solve problems related to distances, angles, and dimensions in these fields.

Q: What are Pythagorean triples?

A: Pythagorean triples are sets of three positive integers that satisfy the Pythagorean Theorem's equation \(a^2 + b^2 = c^2\). Examples include (3, 4, 5) and (5, 12, 13).

Q: How does the trigonometry proof differ from other proofs?

A: The trigonometry proof of the Pythagorean Theorem uses trigonometric functions and identities to demonstrate the theorem's validity. It provides a unique perspective that complements other proofs, such as geometric and algebraic proofs.

Conclusion

The Pythagorean Theorem Trigonometry Proof is a compelling demonstration of the interconnectedness of mathematical concepts and the power of trigonometry in solving geometric problems. By exploring this proof, we gain a deeper understanding of the theorem itself and its applications in various fields. From architecture to physics, the theorem plays a crucial role in solving practical problems and making informed decisions.

As we have seen throughout this article, the Pythagorean Theorem is not just a theoretical mathematical principle; it is a versatile and powerful tool that has stood the test of time. Its simplicity and elegance continue to inspire mathematicians, educators, and learners alike, making it a fundamental concept in the study of mathematics and geometry.

By understanding the Pythagorean Theorem and its trigonometry proof, we can appreciate the beauty and power of mathematical reasoning and its relevance in our everyday lives. Whether in the classroom, the workplace, or the world at large, the theorem remains an essential tool for solving problems and making discoveries, ensuring its continued significance and importance in the future.

For further reading and exploration, visit Math is Fun - Pythagorean Theorem.